Multiphase flow may involve the flow of a gas-liquid, liquid-liquid, liquid-solid, gas-solid, gas-liquid-liquid, gas-liquid-solid, or gas-liquid-liquid-solid mixture. This series of blog posts mainly focuses on gas-liquid and liquid-liquid mixtures, although it also briefly discusses solid-gas and solid-liquid mixtures. We will also review the models and modeling strategies that are available in the CFD and Microfluidics modules.
Multiphase Flow Modeling on Different Scales
The study of multiphase flows with mathematical modeling may be done at several scales. The smallest scale can be around fractions of micrometers, while the largest scales are up to meters or tens of meters. These scales can span about eight orders of magnitude, where the largest length scale may be a hundred million times larger than the smallest scales. This implies that it is numerically impossible to resolve multiphase flows from the smallest to the largest scales using the same mechanistic model throughout the whole range of scales. For this reason, the modeling of multiphase flow is usually divided into different scales.
On the smaller scales, the shape of the phase boundary may be modeled in detail; for example, the shape of the gas-liquid interface between a gas bubble and a liquid. Such models may be referred to as separated multiphase flow models in the COMSOL® software. Methods used to describe such models are usually referred to as surface tracking methods.
On the larger scales, it is impossible to solve the model equations if the phase boundary has to be described in detail. Instead, the presence of the different phases is described using fields, such as volume fractions, while interphase effects such as surface tension, buoyancy, and transport across phase boundaries are treated as sources and sinks in the model equations of so-called dispersed multiphase flow models.
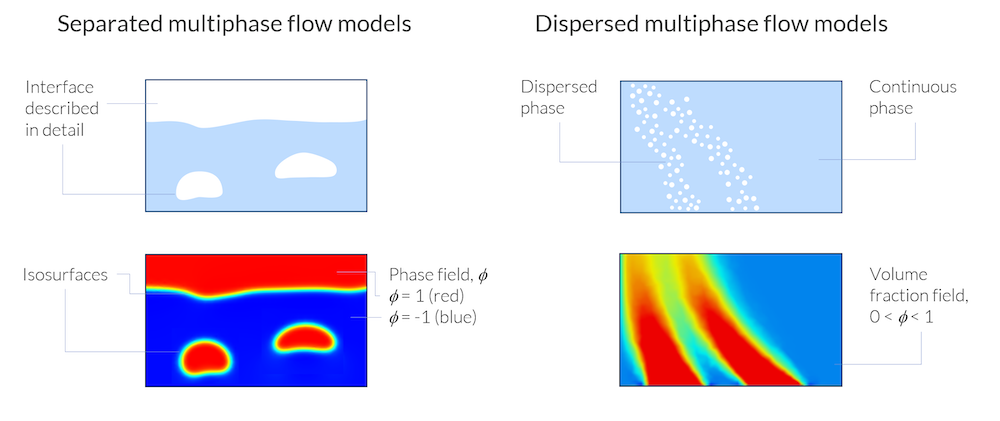
![Multiphase flow models A side-by-side diagram comparing separated and dispersed multiphase flow models.]()
Separated multiphase flow models describe the phase boundary in detail, while dispersed multiphase flow models only deal with volume fractions of one phase dispersed in a continuous phase.
The figure above shows the principal difference between the two approaches for separated and dispersed multiphase flow models. In both exemplified cases, a function, Φ, is used to describe the presence of the gas and liquid phases. However, in the separated multiphase flow model, the different phases are exclusive, and there is a sharp phase boundary between them where the phase field function, Φ, changes abruptly. The phase field function does not have a physical meaning other than keeping track of the location of the phase boundaries.
In the dispersed multiphase flow model, the function Φ describes the local average volume fraction of gas, the dispersed phase, in the liquid, the continuous phase. The average volume fraction can smoothly find values between 0 and 1 everywhere in the domain, signifying if there are small or large amounts of bubbles in the otherwise homogenized domain. In other words, in the dispersed multiphase flow models, the gas and liquid phases can be defined in the same point in space and time, while in the separated multiphase flow models, there is either gas or liquid at a given point and time.
Separated Multiphase Flow Models
There are three different interface tracking methods in the COMSOL Multiphysics® software for separated multiphase flow models:
- Level set
- Phase field
- Moving mesh
The level set and phase field methods are both field-based methods in which the interface between phases is represented as an isosurface of the level set or phase field functions. The moving mesh method is a completely different approach to the same problem. With this approach, the phase boundary is modeled as a geometrical surface separating two domains, with one phase on each side in the corresponding domains.
The field-based problems are usually solved on a fixed mesh. The moving mesh problems are obviously solved using a moving mesh.
The animation below shows the results from a model in which an emulsion is produced in a T-shaped microchannel, where the problem is solved with the phase field method. We can see in this animation that the phase boundary does not coincide with the faces and edges of the mesh. The phase boundary is represented by the isosurface of the phase field function.
The finite element mesh does not have to coincide with the phase boundary between two phases in the phase field and level set methods.
In contrast, the figure below shows the verification model of a rising bubble with moving mesh. The mesh follows the shape of the phase boundary and the edges coincide with this boundary. We can also see the drawback of the moving mesh model. The bubble deforms to such an extent that two secondary bubbles detach from the mother bubble. At this point, the original phase boundary has to be divided into several boundaries. The logic for that is not completely straightforward and this is not yet implemented in the COMSOL® software. Hence, the moving mesh method in the COMSOL® software cannot deal with topology changes. The phase field methods do not have this drawback and can handle any changes in shape of the phase boundary.
The rising bubble verification problem. A topology change occurs when two secondary bubbles break away from the mother bubble.
When Do We Use Field-Based Methods Vs. Moving Mesh?
Moving mesh methods allow for a higher accuracy for a given mesh. The fact that we can apply forces and fluxes directly on the phase boundary is an advantage in this respect. The field-based methods require a dense mesh around the interphase surface in order to resolve the isosurface that defines this surface. It is difficult to define an adaptive mesh that accurately follows the isosurface, which leads that the mesh usually has to be dense in a large volume around the isosurface. This lowers the performance of the field-based methods in relation to moving mesh for the same accuracy. So, when do we use the different methods?
- For microfluidic systems where topology changes are not expected, then the moving mesh method is usually preferable
- In cases where topology changes are expected, then a field-based method has to be used:
- When the effects of surface tension are large, then the phase field method is the preferred method
- When surface tension can be neglected, then the level set method is preferred
Separated Multiphase Flow Models and Turbulence Models
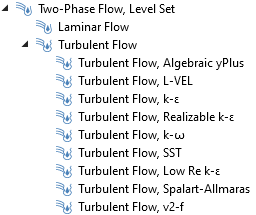
In cases where turbulence models are used, the details of the flow are lost, since only the mean velocity and pressure are resolved. With this in mind, effects of surface tension also become less important for the macroscopic description of the flow. Since turbulence also implies that the flow is relatively vigorous, also at the surface, it is almost impossible to avoid topology changes. Hence, for turbulent flow models and separated multiphase flow combinations, the level set method is preferred. Both the level set and phase field methods can be combined with all turbulence models in COMSOL Multiphysics, as seen in the figure and animation below.
![A screenshot showing a list of Two-Phase Flow, Level Set interfaces in COMSOL Multiphysics.]()
All turbulence models can be combined with the phase field and level set methods for two-phase flow in COMSOL Multiphysics.
Two-phase flow with water and air in a reactor modeled using the level set method in combination with the k-e turbulence model.
Dispersed Multiphase Flow Models
In cases where the phase boundaries cannot be resolved due to their complexity, dispersed multiphase flow models have to be used.
The CFD Module provides four different (in principle) models:
- Bubbly flow model
- For small volume fractions of a light phase in a denser phase
- Mixture model
- For a small volume fraction of a dispersed phase (or several dispersed phases) in a continuous phase that has about the same density as the dispersed phase or phases
- Euler–Euler model
- For any type of multiphase flow
- Can handle any type of multiphase flow also dense particles in gases; for example, in fluidized beds
- Euler–Lagrange models:
- For a relatively small number (tens of thousands, not billions) of bubbles, droplets, or particles suspended in fluid
- Each bubble, particle, droplet, or particle is modeled with an equation that defines the force balance of each particle in the fluid
When Do We Use the Different Dispersed Flow Multiphase Flow Models?
Bubbly Flow
The bubbly flow model is obviously used for gas bubbles in liquids. Since the momentum contribution from the dispersed phase is neglected, the model is only valid when the dispersed phase has a density that is several orders of magnitude smaller than the continuous phase.
Mixture
The mixture model is similar to the bubbly flow model, but it accounts for the momentum contribution of the dispersed phase. It is commonly used for modeling gas bubbles or solid particles dispersed in a liquid phase. The mixture model can also handle an arbitrary number of dispersed phases. Both the mixture model and the bubbly flow model assume that the dispersed phase is in equilibrium with the continuous phase; i.e., the dispersed phase cannot accelerate relative to the continuous phase. Hence, the mixture model cannot handle large solid particles dispersed in a gas.
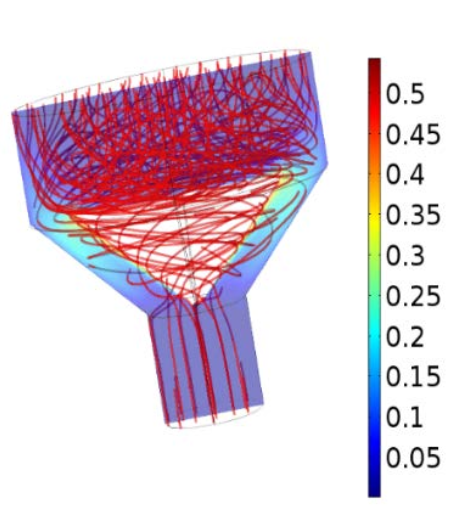
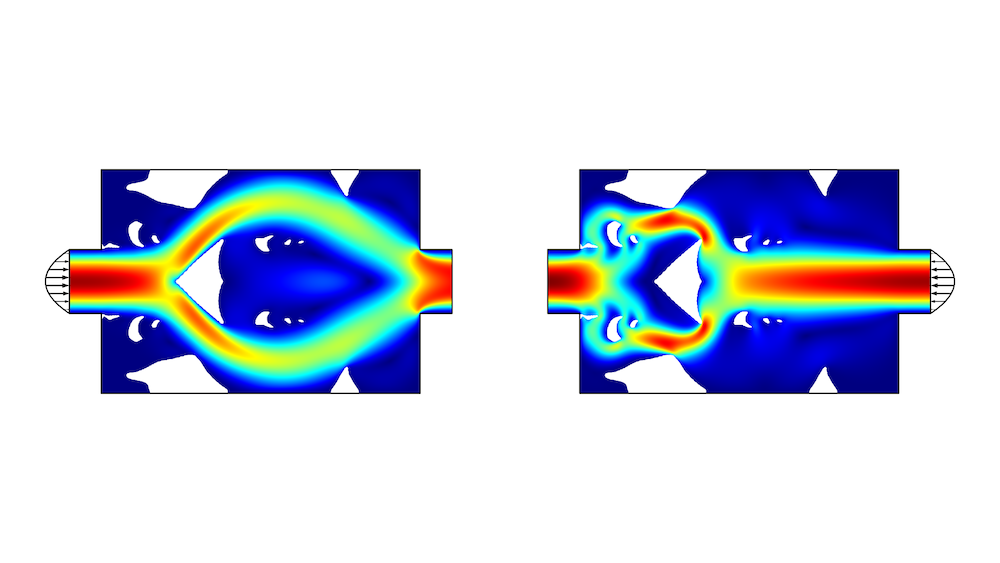
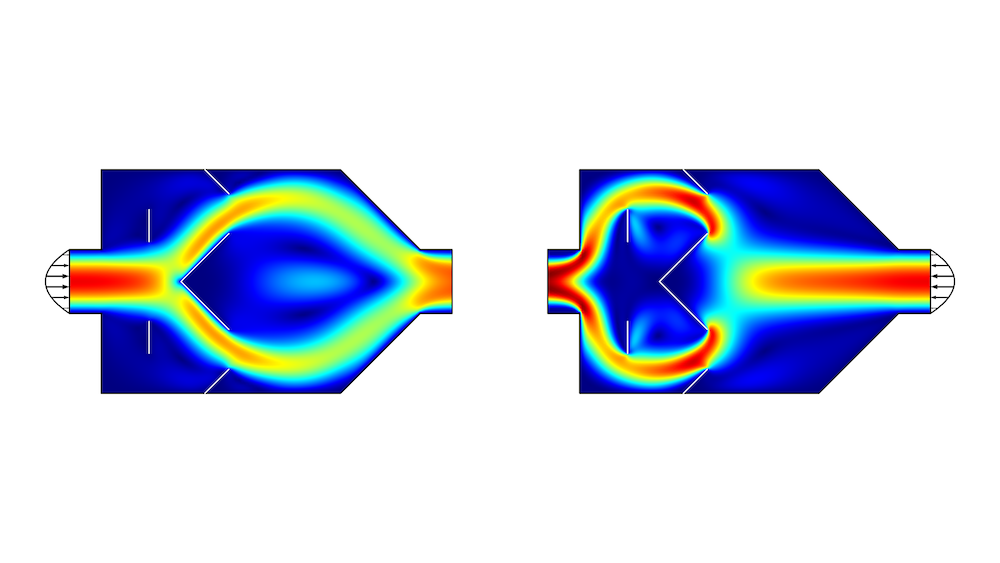
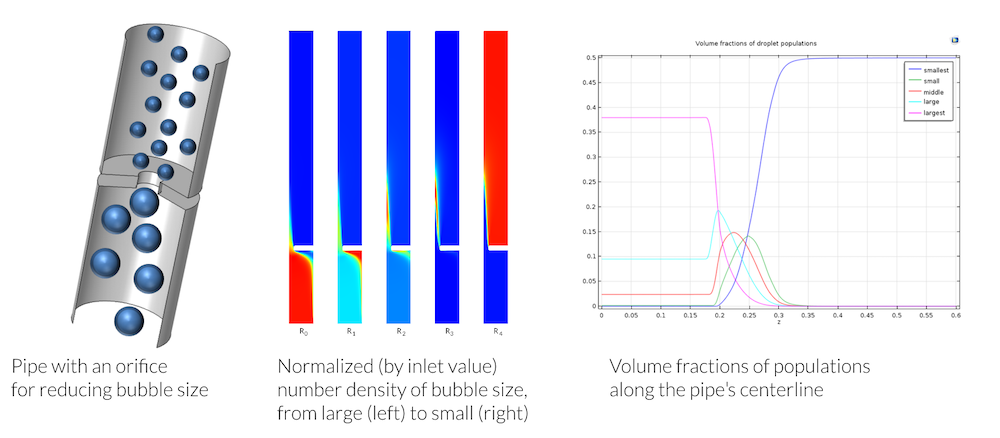
![Mixture model Three side-by-side image showing different examples of modeling multiphase flow with the Mixture model.]()
The mixture model used to model 5 different sizes of bubbles as the multiphase flow mixture is forced through an orifice. The shear in the flow causes larger bubbles to break up into smaller ones.
Euler–Euler
The Euler–Euler model is the most accurate dispersed multiphase flow model and also the most versatile. It can handle any type of dispersed multiphase flows. The dispersed phase is allowed to accelerate, and there is no real limit in the volume fractions for the different phases. However, it defines one set of Navier–Stokes equations for each phase.
In practice, the Euler–Euler model is only applicable for two-phase flow and even then, it is an expensive model with respect to computational cost (CPU time and memory). It is also relatively difficult to work with and requires good initial conditions to get convergence in the numerical solution.
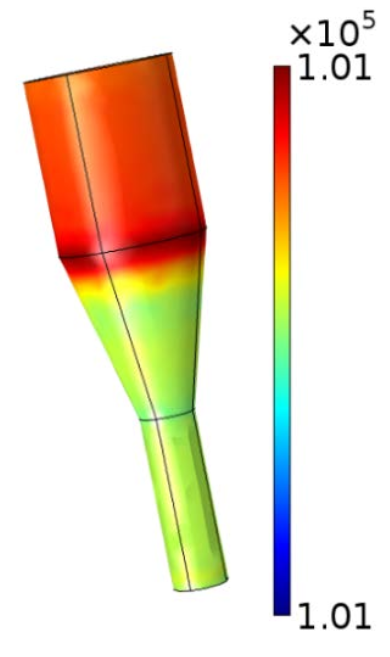
Volume fraction of solid particles in a fluidized bed modeled using the Euler–Euler multiphase flow model.
Euler–Lagrange
When we have a few (tens of thousands but not billions) very small bubbles, droplets, or particles suspended in a continuous fluid, we may be able to use Euler–Lagrange models to simulate a multiphase flow system. These methods have the benefit of being relatively inexpensive, computation-wise. These models are usually also “nice” from a numerical point of view. They are therefore preferred when there is a relatively small number of particles of a dispersed phase in a continuous fluid.
Note that there are also methods to mimic a larger number of particles with Euler–Lagrange methods, using interaction terms and volume fractions that may mimic a system with billions of particles. These methods can be implemented in COMSOL Multiphysics, but they are not available in the predefined physics interfaces.
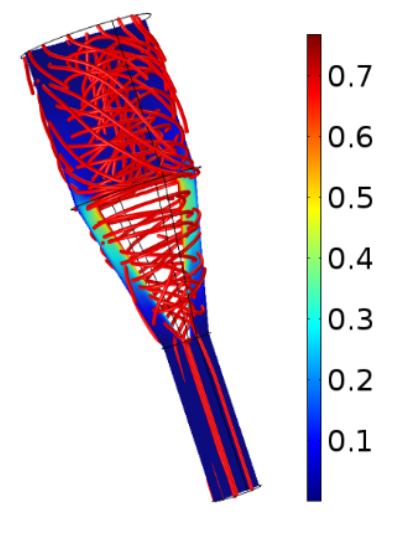
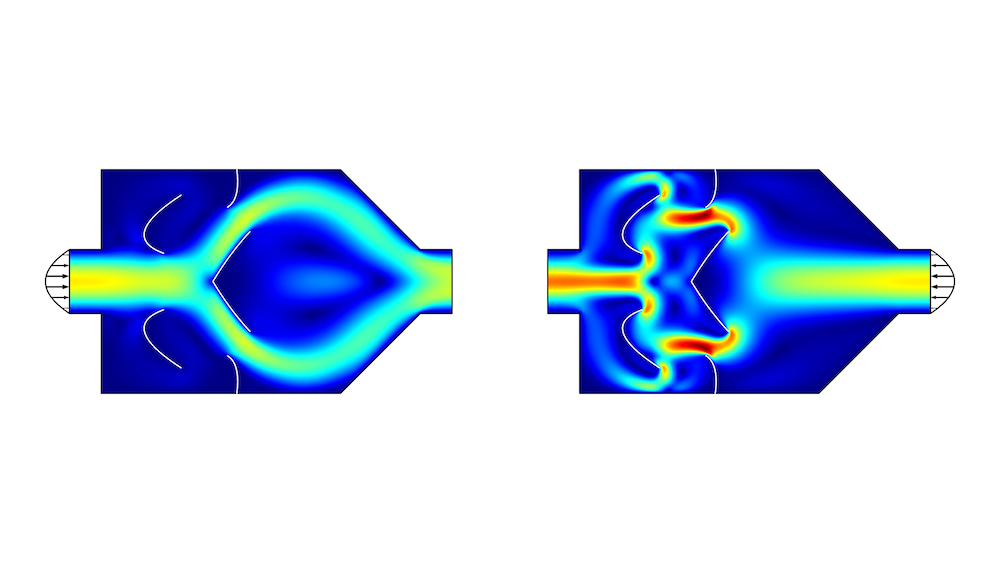
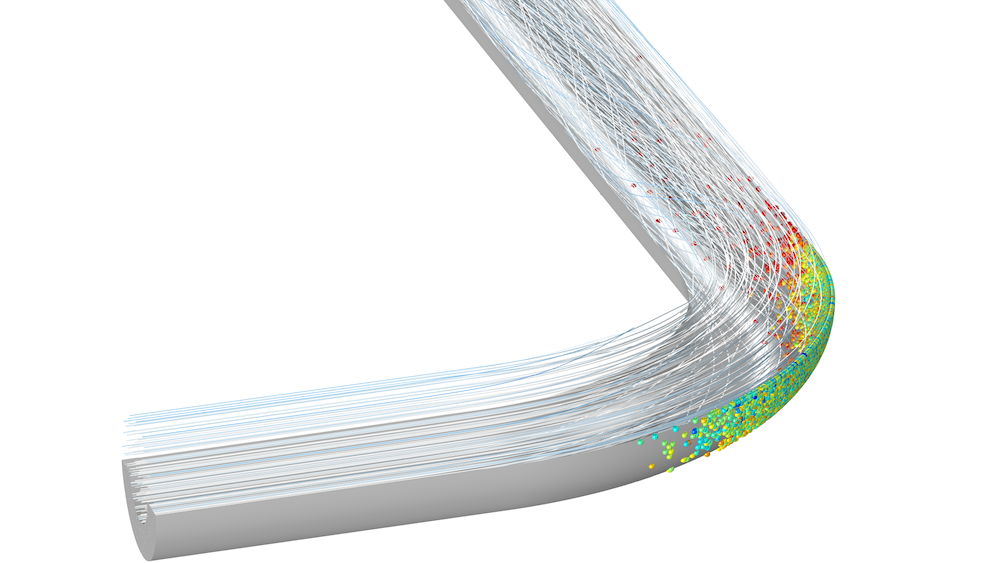
![An image of a model showing particle flow in a pipe bend.]()
Euler–Lagrange multiphase flow models in COMSOL Multiphysics are available with the add-on CFD Module and Particle Tracing Module.
The mixture model is able to handle any combination of phases and is also computationally inexpensive. In most cases, it is advised that we start with this model, unless we deal with systems like fluidized beds (large particles with high density and high volume fractions of the dispersed phase), which can only be modeled with Euler–Euler models.
Dispersed Multiphase Flow Models and Turbulence
The dispersed multiphase flow models are approximative in their nature and fit very well with turbulence models, which are also approximative. It is possible to introduce interactions between dispersed phases and the continuous phase as well as between the bubbles, droplets, and particles in the dispersed phases. These interactions can have their origin in the turbulent eddies modeled with the turbulence model. The bubbly flow, mixture, and Euler–Lagrange multiphase flow models can be combined with all turbulence models in COMSOL Multiphysics. The Euler–Euler multiphase flow model is only predefined for the standard k-e turbulence models with realizability constraints.
![A screenshot of the interfaces for combining the Mixture model and turbulence models.]()
The mixture model can be combined with any turbulence model in COMSOL Multiphysics.
Concluding Remarks
Solving the numerical model equations for multiphase flow may be a very demanding task, even with access to supercomputers. If there were no computer power limitations, the surface tracking methods would be used for all types of mixtures. In reality, these models are limited to microfluidics and for the study of free surfaces of viscous liquids.
The dispersed multiphase flow methods allow for the studying of systems with millions and billions of bubbles, droplets, or particles. But even the simplest dispersed multiphase flow models can generate very complex and demanding model equations. The development of these models into variations that are well adapted to describe specific mixtures has allowed for engineers and scientists to study multiphase flow with a relatively good accuracy and with reasonable computational costs.
Stay tuned as we continue our discussion of multiphase flow simulation on the blog!